Here we will learn about the hypotenuse including how to find the length of the hypotenuse, how to use the hypotenuse to find other missing sides and angles in right angle triangles and how to calculate other values such as the volume or perimeter using the hypotenuse.
There are also hypotenuse worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
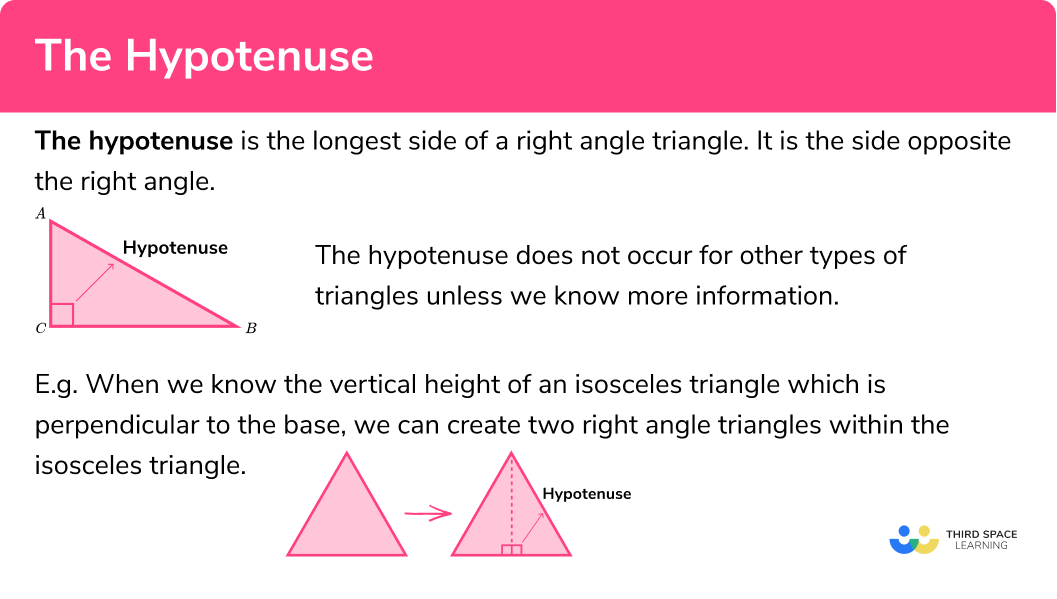
The hypotenuse is the longest side of a right angle triangle. It is the side opposite the right angle.
When we know the vertical height of an isosceles triangle which is perpendicular to the base, we can create two right angle triangles within the isosceles triangle.

We can also calculate diagonals in 2D and 3D shapes by recognising right-angle triangles.
We can find the diagonal length AC of a parallelogram or the diagonal length AH in the cuboid below.
We need to be able to interpret problems and recognise whether we need to use Pythagoras theorem in 2D, 3D, or one of the three trigonometric ratios.
This flow chart describes the information you need to know about a shape in order to solve the problem.
It is important to recognise that with most of these problems, you may need to use the Pythagorean theorem, or trigonometry, or both within the same question so you must be confident with these topics individually to access this topic fully.
Below is a summary of this information,
| Name | Used to find. . . | Rule or formula |
|---|---|---|
| Pythagoras theorem in 2D | The hypotenuse (c) A shorter side (a) | \\c=\sqrt+b^> \\a=\sqrt |
| Sine function | Missing side: Hypotenuse (H) or Opposite (O) | \\H=\frac\\ \\O=H\times\sin(\theta) |
| Cosine function | Missing side: Hypotenuse (H) or Adjacent (A) | \\H=\frac\\ \\A=H\times\cos(\theta) |
| Tangent function | Missing side: Adjacent (A) or Opposite (O) | \\A=\frac\\ \\O=A\times\tan(\theta) |
| Inverse sine function | Missing angle ( \theta ) | \theta=\sin^(\frac) |
| Inverse cosine function | Missing angle ( \theta ) | \theta=\cos^(\frac) |
| Inverse tangent function | Missing angle ( \theta ) | \theta=\tan^(\frac) |
| Pythagoras theorem in 3D | The diagonal (D) | \\D=\sqrt |
In order to calculate the hypotenuse of any right angle triangle:


Get your free hypotenuse worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free hypotenuse worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Calculate the value of x to 1 decimal place.
We know two missing sides of the right angle triangle and no other angles so we can use Pythagoras theorem.
2 Label the right angle triangle (abc or OAH) and state the formula/rule used.
As we are using Pythagoras theorem, label the sides a, b, and c (the opposing side to the right angle).
Pythagoras theorem, c=\sqrt+b^> .
3 Calculate the missing angle or side.
Calculate the length of the hypotenuse of a right triangle, x , to 1 decimal place.
Determine whether to use Pythagoras theorem or trigonometry.
We know one missing side of the right angle triangle and one acute angle so we can use trigonometry to find the hypotenuse.
Label the right angle triangle (abc or OAH) and state the formula/rule used.
As we are using trigonometry, label the sides opposite, adjacent and hypotenuse according to the location of the known angle.
The two important sides in this question are the opposite side (O) and the hypotenuse (H) so we need to use the sine function to calculate the value of x .
Calculate the missing angle or side.